

Fresadoras
Lección 15ª
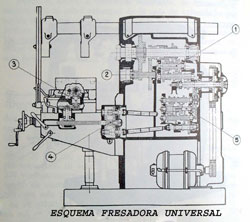 Las fresadoras son máquinas-herramientas cúyo útil cortante lo forman discos, o cilindros de acero al carbono (de escaso empleo en la actualidad), acero rápido y metal duro, asi como platos con insertos de placas de carburo metálico o metal duro.
Las fresadoras son máquinas-herramientas cúyo útil cortante lo forman discos, o cilindros de acero al carbono (de escaso empleo en la actualidad), acero rápido y metal duro, asi como platos con insertos de placas de carburo metálico o metal duro.Existen varios modelos de fresadoras , entre los que destacan las Fresadoras Horizontales, las Verticales y las Universales
La fresadora, puede que sea la maquina más completa, por la cantidad de trabajos que pueden ser realizados con élla, entre los mísmos podemos enumerar los siguientes: Planeado, Ranurado, Ranurado en T, Fresado de Chaveteros y Paliers, Tallado de Engranajes (rectos, inclinados, helicoidales), Tallado de levas y excéntricas, ect.
 El equipamiento de accesorios, es asi mismo muy completo, pero la inversión más grande, es la que corresponde a la herramienta ( aunque lógicamente cada fresador la adquirirá según las necesidades de sus trabajos).
El equipamiento de accesorios, es asi mismo muy completo, pero la inversión más grande, es la que corresponde a la herramienta ( aunque lógicamente cada fresador la adquirirá según las necesidades de sus trabajos).Las piezas a mecanizar, se sujetan sobre la mesa de trabajo mediante la mordaza (que puede ser mecánica o hidráulica ), colocadas en el plato de tres garras (igual al del torno, y que va montado en el Aparato Divisor Universal ), o embridada a la mesa.
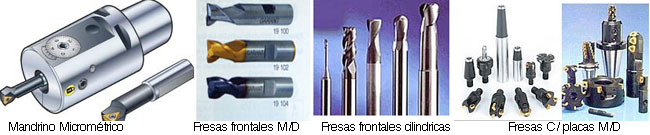
Las fresas presentan formas muy variadas, para según que trabajos tengamos que realizar. Podemos hacer una primera clasificación:

Fresas para labrar herramientas (brocas, machos de roscar, escariadores, mandriles, etc.
Fresas para ranuras en T.
Fresas para ranuras en cola de milano.
Fresas para mecanizar chaveteros
Fresas para ejes estriados (palier).
Fresas para roscar.
Fresas para avellanados.
Fresas de módulo para tallar engranajes (Rectos y Helicoidales) Estas fresas están formadas por juegos de 8, y de 15 unidades con forma del perfil del diente correspondiente al nº de dientes del engranaje a fabricar.
Las herramientas, se montan en el eje horizontal, con sus casquillos separadores y tuerca de aprieto en el caso de discos, en los conjuntos pinzas-portapinzas, o en los conos normalizados I.S.O.
En los trabajos realizados con fresadora, debemos prestar especial atención a la velocidad de corte de la herramienta, a la velocidad de avance de la mesa, al sentido del recorrido de la mesa y a la sujeción de la pieza
Una vez colocada la pieza en la mordaza (por ejemplo), y montada la herramienta en el eje horizontal o en el Cabezal Universal, procederemos al cálculo del número de revoluciones a que debe girar la herramienta:
 r.p.m. = (V.c.x 1000) / (3,14 x D)
r.p.m. = (V.c.x 1000) / (3,14 x D)Recordemos que: V.c. es la velocidad de corte de la hta en mts/minuto
 D, es el diámetro de la hta. en m.m.
D, es el diámetro de la hta. en m.m.Respecto a las condiciones de la mesa, la velocidad de avance pude ser en en mm. por minuto, o por mm. por revolución.
Respecto al sentido de avance, puede ser en:
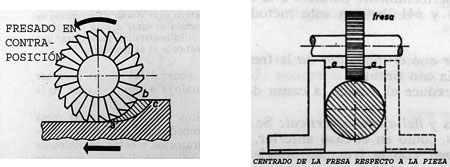
Contraposición, o en concordancia.
Se recomienda trabajar en contraposición, para que la fresa no adelante bruscamente sobre la pieza, a causa de la holgura de la tuerca sobre el husillo de la mesa, provocando la rotura de dientes en la fresa
Accesorios de la Fresadora.
 Entre los accesorios de la Fresadora, debemos destacar, los aparatos divisores, con los cuales, podemos realizar ranuras equidistantes sobre piezas cilíndricas (por ejemplo: polígonos, chaveteros engranajes, etc.) El utilizado preferentemente es el Aparato Divisor de Visinfin con Círculo de Agujeros, o Aparato Divisor Universal. La relación entre el Visinfin y la corona dentada a la que va acoplado el plato de tres garras, es de 1/40, o también 1/60.
Entre los accesorios de la Fresadora, debemos destacar, los aparatos divisores, con los cuales, podemos realizar ranuras equidistantes sobre piezas cilíndricas (por ejemplo: polígonos, chaveteros engranajes, etc.) El utilizado preferentemente es el Aparato Divisor de Visinfin con Círculo de Agujeros, o Aparato Divisor Universal. La relación entre el Visinfin y la corona dentada a la que va acoplado el plato de tres garras, es de 1/40, o también 1/60.El plato con el circulo de agujeros, no siempre está fijo al aparato divisor, a veces puede recibir movimientos giratorios mediante trenes de engranajes, que unas veces enlazan con el husillo de la mesa, y otras con el eje portapiezas.
Cuando se enlazan con engranajes el circulo de agujeros con el husillo de la mesa, podemos construir ranuras helicoidales, ya que la pieza tiene entonces dos movimientos simultaneos,
 uno de traslación y otro de rotación. Para que esto se realice, se introduce el índice de la manivela en uno de los agujeros del plato,( de ésta manera al girar el husillo, será arrastrada la manivela-el disco-la pieza, la cual a la vez que avanza también gira) La regla para calcular los engranajes para construir ranuras helicoidales se expone al final de la presente lección.
uno de traslación y otro de rotación. Para que esto se realice, se introduce el índice de la manivela en uno de los agujeros del plato,( de ésta manera al girar el husillo, será arrastrada la manivela-el disco-la pieza, la cual a la vez que avanza también gira) La regla para calcular los engranajes para construir ranuras helicoidales se expone al final de la presente lección.Para realizar la siguiente ranura, se desacopla el índice del plato de agujeros, procediendo del modo que se explica para efectuar divisiones en general.
Cuando se enlazan el plato de agujeros con el eje portapiezas, permite hacer divisiones con el sistema diferencial (a continuación de la construcción de los engranajes rectos)
Veamos con un ejemplo, el funcionamiento del aparato divisor:
Tomemos el de 1/40; para que la pieza sujeta en el plato de tres garras, de una vuelta completa, tenemos que girar la manivela que lleva acoplada, 40 vueltas.
Para realizar divisiones con dichos aparatos, aplicaremos la siguiente regla:
Se forma un quebrado que tenga por numerador la constante del Aparato (40), y por denominador, el número de divisiones que queremos hacer
 40 : 5 = 10
40 : 5 = 10Si quisiéramos mecanizar 6 ranuras, resultaría:
 40 : 6 = 6 + 4/6
40 : 6 = 6 + 4/6Dicho resultado nos indica que para realizar cada ranura, (después de la primera), tenemos que girar la manivela, 6 vueltas enteras además dengranajes elicoidalese 4/6 de vuelta.

Para hacer factible dicho quebrado, elegiremos en el plato de agujeros que lleva el Aparato Divisor uno que sea múltiplo de 6, por ejemplo, el que tenga 30 agujeros, y sobre el mismo, contaremos 20 agujeros (resultado también de multiplicar por 5, el numerador del quebrado) Para mantener dicho recorrido, fijaremos con los índices que lleva el disco, una abertura, que abarque un ángulo con los 20 agujeros calculados, del disco elegido de 30.
Para realizar el mecanizado sucesivo de cada ranura, giraremos la manivela, 6 vueltas, más 20 agujeros del disco que tenga 30 (la abertura del arco comprendido entre los índices)
El procedimiento para construir engranajes es el mismo que el empleado en estos ejemplos. Supongamos que vamos a realizar los cálculos necesarios para obtener un engranaje de 90 dientes:
 40 : 90 = 40 / 90 = 4 / 9
40 : 90 = 40 / 90 = 4 / 9Multiplicando por É5. quedará
 20 / 45,
20 / 45,Que nos indica que para realizar el fresado de cada diente, debemos girar la pieza, el arco formado por el ángulo correspondiente a tomar 20 agujeros, del disco de 45.
Y estando en dichos trabajos, completaremos con el tema acerca de:
Engranajes.
 Generalidades sobre los engranajes.
Generalidades sobre los engranajes.Un engranaje es un mecanismo formado por dos ruedas dentadas, de tal manera construidas, que los dientes de una de ellas, se introducen perfectamente en las ranuras (vanos) de la otra, transmitiendo el movimiento por empuje directo. También se denomina engranaje en el lenguaje ordinario, a cada uno de los componentes del conjunto.
Cuando dos ruedas dentadas de distinto tamaño engranan entre si, la de mayor tamaño recibe el nombre de rueda, y la menor, piñón. Cuando la rueda es de dimensiones considerables tiene unos brazos radiales, que unen la corona (parte donde van los dientes) con el cubo (parte por donde un engranaje se fija a su eje). Los piñones generalmente son macizos, y los que tienen un diámetro algo mayor, se construyen con forma llamados de plato.
Los engranajes se mecanizan (tallan) con fresas de módulo, (que constan de juegos con 8 fresas, o de 15 fresas para los tamaños superiores al módulo 8). Con cada una de las fresas que constituyen el juego, se pueden fresar los engranajes de un Nº determinado de dientes.


| Con la fresa Nº | |
| 1 | de 12 a 13 dientes |
| 2 | de 14 a 16 dientes |
| 3 | de 17 a 20 dientes |
| 4 | de 21 a 25 dientes |
| 5 | de 26 a 34 dientes |
| 6 | de 35 a 54 dientes |
| 7 | de 55 a 134 dientes |
| 8 | de 135 Hasta Cremalleras (que se consideran engranajes con radio infinito) |
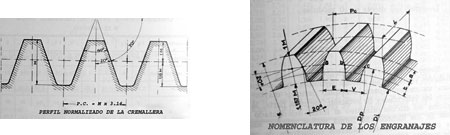
Se denomina Módulo, de un engranaje, al cociente de dividir el diámetro primitivo entre el número de dientes del engranaje. Se expresa en mm.
El módulo es la unidad que se toma para calcular la totalidad de las demás dimensiones de los engranajes.
Los países que utilizan la pulgada en vez del milímetro, para el cálculo, emplean el Diametral Pich .
En todo engranaje, encontramos la siguiente nomenclatura:
Diámetro Exterior.- Corresponde al de la circunferencia donde está inscrito el engranaje.
Diámetro de Fondo.- Es el de la circunferencia donde se apoyan los dientes.
Diámetro Primitivo.- .- Es el que corresponde a la circunferencia donde se produce el punto de tangencia teórica de los dientes de dos engranajes acoplados
Cabeza del Diente.- Es la parte del diente que está sobre la circunferencia primitiva.
Pie del Diente.- Es la parte que está por el interior de la circunferencia primitiva.C
Flanco del Diente.- Es la parte del diente que entra en contacto con el diente del otro engranaje al girar.
Longitud del Diente.- Es el grueso que tiene la corona del engranaje. L
Profundidad del Diente.- Distancia entre las circunferencias exterior e interior.C+B
Espesor del Diente.- Es la anchura del diente, medida sobre la circunferencia primitiva (es la longitud del arco, no de la cuerda) E
Paso Circular.- Se le llama a la distancia entre los centros de dos dientes consecutivos, medida sobre la circunferencia primitiva Pc
Principales tipos de engranajes.
Engranajes Rectos.- Se llaman a los engranajes cilíndricos de diente recto. Transmiten el movimiento entre ejes paralelos. Una variante de éste enunciado, es cuando el movimiento se transmite entre un engranaje exterior y una cremallera.
Engranajes Helicoidales.- Se denominan los engranajes cilíndricos con dientes en hélice. Se emplean para transmitir el movimiento entre ejes paralelos y entre ejes que se cruzan.

Engranajes de Visinfin (o tornillo sin fin).- Son los que se emplean para transmitir el movimiento entre ejes que se cruzan en ángulo recto, y además cuando la relación de velocidades es muy grande.
Engranajes Cónicos.- Se emplean para transmitir el movimiento, entre ejes que se cortan. Los dientes de éstos engranajes pueden ser: rectos, inclinados y en espiral. Una variedad de los engranajes cónicos son los denominados Hipoides.
FORMULAS PARA EL CALCULO DE LOS ENGRANAJES RECTOS.
Para la realización de los cálculos, emplearemos las abreviaturas que se indican a continuación:
| m | módulo | d | diámetro primitivo |
| de | diámetro exterior | df | diámetro de fondo |
| z | número de dientes | p | paso circular |
| e | espesor del diente | h | profundidad del diente |
| hc | altura de la corona | B | longitud del diente |
| C | distancia entre centros | Lt | largo total ocupado por dos en g. |
| n | Nº R.P.M | v | velocidad tangencial cir. Primitiva |
PARA CALCULAR:
 d = z.m
d = z.mp = 3,14.m
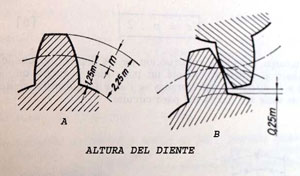
h = 2,16.
h = 2,25.m ; h Para velocidades mas altas
de= (z+2).m
e = p : 2
B = 10.m
d = de - 2m
z = d : m
C = (d1 + d2) : 2
Los nº de revoluciones de dos ruedas dentadas que engranen entre si, estáan en relación inversa a los números de dientes de cada una de ellas.
| n2 / n1 = z1 / z2 | |
| O bien | n1 . z1 = n2 . z2 |
Regla para hacer divisiones por el sistema diferencial
Antes de alejarnos de cómo realizamos las divisiones para la construcción de engranajes, ranuras, polígonos, etc, .tenemos que tener en cuenta, que en ocasiones no es posible aplicar dichos cálculos, por no disponer de discos de agujeros correspondientes. Dicho inconveniente, se solventa, conectando mediante engranajes previamente calculados, el eje de la rueda de visinfin, con el eje que mueve el plato de agujeros.
Entonces, al girar la manivela, girará también el plato de agujeros con los dedos indicadores, unas veces en un sentido, otras veces en el sentido opuesto, según el número de engranajes que se monten.
En el primer caso se correrán más espacios que si el disco estuviese fijo, y en el segundo caso , menos.
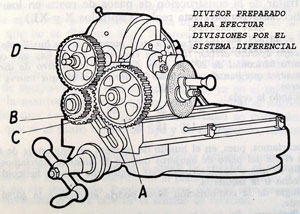 El engranaje D, va montado en el eje de la rueda de visinfin; el engranaje A, va montado en el eje que da movimiento al plato. Los engranajes B y C, se colocan en un eje intermedio. Puede colocarse además otro engranaje en un cuarto eje intermediario, para invertir el movimiento de rotación.
El engranaje D, va montado en el eje de la rueda de visinfin; el engranaje A, va montado en el eje que da movimiento al plato. Los engranajes B y C, se colocan en un eje intermedio. Puede colocarse además otro engranaje en un cuarto eje intermediario, para invertir el movimiento de rotación.Realicemos un ejemplo: Tallar un engranaje de 43 dientes, en una fresadora cuyo aparato divisor tiene una constante de 60.
Apliquemos la regla:
 60 : 43 = 1 + 17/43
60 : 43 = 1 + 17/43Suponemos que no tenemos disco de 43 agujeros,( ni de sus múltiplos), con lo cual no podemos resolver por la regla general nuestro problema.
Buscamos un número de dientes inmediato superior o inferior a 43, que pueda construirse aplicando la regla general; pongamos 45:
 60 : 45 = 1 +15/45 = 1 + 5/15 = 1+ 10/30
60 : 45 = 1 +15/45 = 1 + 5/15 = 1+ 10/30Como suponemos que disco de 30 agujeros si que lo tenemos, para la realización de cada diente, debemos dar a la manivela, una vuelta y además, 10 espacios del disco con 30 agujeros.
Los engranajes que deben enlazar el eje de la rueda de visinfin, con el eje que mueve el plato de agujeros, responderán a la siguiente proporción:
 45 : (45-43) = 60 :X
45 : (45-43) = 60 :X45 : 2 = 60 : X
| Donde: | 43, es el nº de dientes que pretendemos construir. |
| 45, es el nº de dientes inmediato superior que se puede construir | |
| 60, es la constante del aparato divisor. | |
| X = (60 x 2) : 45 = 120/45 =24/9 =8/3 =80/30 |
Colocaremos la rueda de 80 dientes en el eje de la rueda de visinfin y la de 30, en el eje que mueve el plato de agujeros. Montamos las ruedas intermediarias necesarias, para que el plato gire en el mismo sentido que la manivela.
Para pasar de un diente a otro, giraremos la manivela una vuelta y 10 espacios del disco que tiene 30.
FORMULAS PARA EL CÁLCULO DE ENGRANAJES HELICOIDALES
En los engranajes helicoidales, el paso (distancia entre los centros de dos dientes consecutivos, medida sobre la circunferencia primitiva), se toma de dos maneras: perpendicular al eje del engranaje o perpendicular al diente. En el primer caso se llama paso circunferencial (pc), y en el segundo paso normal (pn).
Para facilidad de construcción, se hace siempre que el modulo normal coincida con uno de los módulos normalizados de los engranajes rectos
Un engranaje helicoidal es un tornillo de tantas entradas como dientes tiene. El paso de de rosca de éste tornillo, se llama paso helicoidal del engranaje (H). El ángulo de inclinación es el ángulo agudo que forma el diente con el eje del engranaje y se representa con la letra griega BETA .(ß)
Es importante observar previamente que el diámetro primitivo de un engranaje helicoidal, se deriva de las dimensiones del módulo circunferencial y en cambio la altura del diente y otras proporciones con que se hacen los engranajes, se derivan de las dimensiones del modulo normal.
Una relación fundamental de la que se derivan otras relaciones es la siguiente:
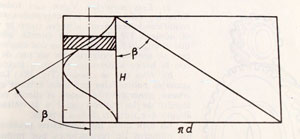
Pn = pc . cos ß
En la figura adjunta se ve que el paso normal es el cateto de un triangulo rect´angulo, cuya hipotenusa es el paso circunferencial y por Trigonometria se deduce que un cateto es igual a la hipotenusa por el coseno del ´angulo comprendido.
De la f´ormula anterior se deducen las siguientes:

| mn= | mc . cos.ß |
| d= | z . mc |
| h= | 2,25 . mn |
| de= | d + 2 . mn |
La relación que nos permite hallar el paso helicoidal es la siguiente:
Π . d = H . tg ß

Esta f´ormula la podemos razonar así:
Si desarrollamos (como se ve en la figura anterior, el cilindro correspondiente a la circunferencia primitiva, observamos que se forma un triangulo rect´angulo, en el cual uno de los catetos es el desarrollo de la circunferencia Π . d y el otro es el paso helicoidal. Aplicando a éste triangulo las reglas de Trigonometria, resulta la formula antedicha:
 Π . d = H . tg ß
Π . d = H . tg ßRecopilación de formulas de los engranajes helicoidales :
| Pn= | pc . cos ß | d= | z . mn / cos ß | |
| Mn= | mc .cos ß | pc= | Π . mc | |
| d= | z . mc | mc= | mn/ cos ß | |
| h= | 2,25 . mn | pn= | Π . mn | |
| de= | d + 2 . mn | H= | Π . d /tg ß | |
| Πd= | H . tg ß | H= | mn . z . Π /sen ß |
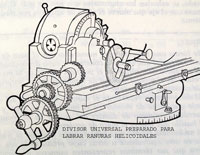
REGLA PARA CALCULAR LOS ENGRANAJES NECESARIOS PARA CONSTRUIR RANURAS HELICOIDALES.-
Se forma una fracción cuyo numerador sea el paso de la ranura helicoidal que se pretende construir, y cuyo denominador sea el producto de multiplicar el paso del husillo de la mesa, expresado en el mismo sistema de unidades que el anterior, por la constante del aparato divisor.
 El denominador representa el número de dientes del engranaje que se ha de montar en el husillo de la mesa, y el numerador, el número de dientes del engranaje que se ha de montar en el husillo que mueve el plato de agujeros. En el caso de no tener dicha relación de engranajes, se transformará la fracción en otra equivalente.
El denominador representa el número de dientes del engranaje que se ha de montar en el husillo de la mesa, y el numerador, el número de dientes del engranaje que se ha de montar en el husillo que mueve el plato de agujeros. En el caso de no tener dicha relación de engranajes, se transformará la fracción en otra equivalente.Si la ranura que se crea fuese de sentido contrario al deseado, se colocara una rueda dentada intermedia.
EJEMPLO:
En una fresadora con paso de husillo de la mesa de p= 5 mm., y el aparato divisor tiene la constante de k=40, tenemos que construir un engranaje helicoidal con paso helicoidal de H=500 mm. Calcular los engranajes necesarios.

Montaremos la rueda de 40 dientes en el eje del husillo de la mesa, el engranaje de 100 dientes en el husillo que mueve el plato de agujeros. La rueda intermedia que transmite el movimiento se montará en la lira o guitarra correspondiente.
Como ya indicamos si la ranura debiese ser en la dirección inversa, se montaría otra intermedia conectando con la primera.

Para ampliar conocimientos de los temas: Contactar on line
El contenido de este manual está dedicado a uso personal del lector, no con fines lucrativos del mismo.
A continuación si lo desa puede descargarse la lección.




